漢明碼
維基百科,自由的百科全書
| 此條目已列出參考文獻,但因爲沒有文內引註而使來源仍然不明。(2013年3月2日) |
漢明碼(Hamming Code),是在電信領域的一種線性偵錯碼,以發明者Richard Hamming的名字命名。漢明碼在傳輸的訊息流中插入驗證碼,以偵測並更正單一位元錯誤。由於簡單的漢明編碼,它們被廣泛應用於內存(RAM)。其 SECDED (single error correction, double error detection) 版本另外加入一檢測位元,可以偵測兩個以下同時發生的位元錯誤,並能夠更正單一位元的錯誤。因此,當傳送端與接收端的位元樣式的漢明距離 (Hamming distance) 小於或等於1時(僅有 1 bit 發生錯誤),可實現可靠的通訊。相對的,簡單的奇偶檢驗碼除了不能糾正錯誤之外,也只能偵測出奇數個的錯誤。
目錄[隱藏] |
[編輯]歷史
1940年,漢明於貝爾實驗室(Bell Labs)工作,運用貝爾模型V(Bell Model V)電腦,一個週期時間在幾秒鐘內的機電繼電器機器。輸入端是依靠打孔卡(Punched Card),這不免有些讀取錯誤。在平日,特殊代碼將發現錯誤和閃燈(flash lights),使得操作者能夠糾正這個錯誤。在週末和下班期間,在沒有操作者的情況下,機器簡單的轉移到下一個工作。
漢明在週末工作,他對於不可靠的讀卡機總是必須重新開始專案變得愈來愈沮喪。在接下來的幾年中,他為了解決偵錯的問題,開發了功能日益強大的偵錯演算法。在1950年,他發表了至今所稱的漢明碼。現在漢明碼有著廣泛的應用。
[編輯]漢明碼之前
有多種檢查錯誤的編碼方式在漢明碼出現之前被使用,但是沒有一個可以在和漢明碼相同空間消耗的情況下,得到相等的效果。
[編輯]奇偶
奇偶校驗是一種添加一個奇偶位用來指示之前的資料中包含有奇數還是偶數個1的檢驗方式。如果在傳輸的過程中,有奇數個位發生了改變,那麼這個錯誤將被檢測出來(注意奇偶位本身也可能改變)。一般來說,如果資料中包含有奇數個1的話,則將奇偶位設定為1;反之,如果資料中有偶數個1的話,則將奇偶位設定為0。換句話說,原始資料和奇偶位組成的新資料中,將總共包含偶數個1.
奇偶校驗並不十分健壯,如果資料中有偶數個位發生變化,則奇偶位仍將是正確的,因此不能檢測出錯誤。而且,即使奇偶校驗檢測出了錯誤,他也不可以指出哪一位出現了錯誤,從而進行更正。資料必須整體丟棄並且重新傳輸。在一個噪音較大的媒介中,成功傳輸資料可能需要很長時間或者不可能完成。雖然奇偶校驗的效果不佳,但是由於他只需要一位額外的空間開銷,因此這是開銷最小的檢測方式。並且,如果知道了發生錯誤的位,奇偶校驗還可以恢複數據。
[編輯]漢明碼
如果一條訊息中包含更多用於糾錯的位,且透過妥善安排這些糾錯位使得不同的出錯位產生不同的錯誤結果,那麼我們就可以找出出錯位了。在一個7位的訊息中,單個位出錯有7種可能,因此3個錯誤控制位就足以確定是否出錯及哪一位出錯了。
漢名研究了包括五取二碼在內的編碼方案,並歸納了他們的想法。
[編輯]通用演算法
下列通用演算法可以為任意位數位產生一個可以糾錯一位(英語:Single Error Correcting)的漢明碼。
- 從1開始給數字的數據位(從左向右)標上序號, 1,2,3,4,5...
- 將這些資料位的位置序號轉換為二進制, 1, 10, 11, 100, 101, 等.
- 資料位的位置序號中所有為二的冪次方的位(編號1,2,4,8,等,即資料位位置序號的二進制表示中只有一個1)是校驗位
- 所有其它位置的資料位(資料位位置序號的二進制表示中至少2個是1)是資料位
- 每一位的資料包含在特定的兩個或兩個以上的校驗位中,這些校驗位取決於這些資料位的位置數值的二進制表示
- 校驗位 1 覆蓋了所有資料位位置序號的二進制表示倒數第一位是1的資料:1(校驗位自身,這裡都是二進制,下同),11,101,111,1001,等
- 校驗位 2 覆蓋了所有資料位位置序號的二進制表示倒數第二位是1的資料:10(校驗位自身),11,110,111,1010,1011,等
- 校驗位 4 覆蓋了所有資料位位置序號的二進制表示倒數第三位是1的資料:100(校驗位自身),101,110,111,1100,1101,1110,1111,等
- 校驗位 8 覆蓋了所有資料位位置序號的二進制表示倒數第四位是1的資料:1000(校驗位自身),1001,1010,1011,1100,1101,1110,1111,等
- 簡而言之,所有校驗位覆蓋了資料位置和該校驗位位置的二進制與的值不為0的數。
採用奇校驗還是偶校驗都是可行的。偶校驗從數學的角度看更簡單一些,但在實踐中並沒有區別。
校驗位一般的規律可以如下表示:
資料位位置 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ... 編碼後資料位置 p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 奇偶校驗位
覆蓋率p1 X X X X X X X X X X p2 X X X X X X X X X X p4 X X X X X X X X X p8 X X X X X X X X p16 X X X X X
觀察上表可發現一個比較直觀的規律:第i個檢驗位是第2i-1位,從該位開始,檢驗2i-1位,跳過2i-1位……依次類推。例如上表中第3個檢驗位p4從第23-1=4位元開始,檢驗4、5、6、7共4位元,然後跳過8、9、10、11共4位元,再檢驗12、13、14、15共4位元……
[編輯]例子
對11000010進行漢明編碼,求編碼後的碼字。
1. 列出表格,從左往右(或從右往左)填入數位,但2的次方的位置不填。
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 資料 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
2. 把資料行有的1的列的位置寫為二進制。
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 資料 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | ||||||
| 二進制 | 0011 | 0101 | 1011 |
3. 收集所有二進制數位,求異或。

4. 把1101依次填入表格中2的次方的位置。
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 資料 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | ||||||
| 二進制 | 0011 | 0101 | 1011 | |||||||||||
| 校驗 | 1 | 1 | 0 | 1 |
5. 所以編碼後的碼字是111010010010。
 ,存在一個編碼,帶有
,存在一個編碼,帶有 個奇偶校驗位
個奇偶校驗位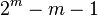 個資料位。該
個資料位。該
沒有留言:
張貼留言