(1) CPU的歷史演進~處理位元的進化在1971年，Intel公司及Marcian E.Hoff共同發表了-4004處理器，它是一個4位元的微處理器，為目前所見各處理器的先驅，主要使用在早期電視遊樂器和小型微處理器為基礎的控制器。到了1974年，Intel提出了延續性相容的版本-8008微處理器，由於其記憶體及指令集仍然很小，使得其可用性受到許多限制，因此在1973年Intel提出了最早的8位元微處理器-8080，其處理速度已較8008快了將近10倍。
1976年，Intel又發表了8086微處理器，約一年後又提出了8088，使用在IBM的個人PC上，兩者均是16位元微處理器，之後又改良出80186、80286，而80286的時脈頻率在Intel最終版時已可達到16MHz，每秒可執行8億個指令數(8MIPS)。之後再進一步演進到80386、80486微處理器的時代，則已邁入32位元的微處理器時代，而到目前為止的Pentium Ⅲ、Pentium Ⅳ時期，CPU依然處於32位元的世代(Pentium系列雖然在外部頻率達到64位元，但是其內部的資料匯流排採用的是32條*2的架構，因此尚不足以稱為真正64位元的處理器)。到了近年來，AMD推出伺服器版所使用的K8 Opteron處理器及針對桌上型電腦推出Athlon 64處理器後，Intel也打出伺服器版的Xeon DP處理器來與AMD抗衡，正式揭開64位元微處理器的世代，相信未來Intel針對一般消費型市場所主打的Pentium Ⅳ處理器勢必也將研發新的晶片以投入64位元處理器的競爭市場。
不過大家也不用陷入位元的迷失之中，因為要能達到處理器最大的效能，必須仰賴作業系統(OS)、記憶體、硬體、匯流排等元件來配合來行，以目前的技術來看，微軟的作業系統在Windows 2003 Beta 1之後才正式走向64位元的作業系統，要達到全面加速的64位元時代，雖不遠但仍需一段時間的努力才行。(2) CPU的組成
指令集：
cpu中可供執行指令的集合，包括精簡指令集及複雜指令集，其他會影響到電腦整體的執行能力 。
cpu中可供執行指令的集合，包括精簡指令集及複雜指令集，其他會影響到電腦整體的執行能力 。
指令暫存器(Instruction Register)，用來存放下一個即將被執行的指令。
一般用途暫存器(General-Purpose Register)，用來暫存一般運算資料及位址資料。
位址暫存器(Address Register)，用來存放指令或資料在記憶體中的位址。
旗標暫存器(Flag)，記錄指令執行的狀態，進而決定程式走向。
程式計數器(Program Counter)，存放下一個要執行的指令所在位址。
CPU是由「矽」晶片製作而成，科學家利用顯微照相技術，將數百萬顆的電晶體所組成的電路縮小至小小的晶片之中。其組成包括控制單元(Contrl Unit)、算術邏輯單元(Arithmetic/Logic Unit)、暫存器(Register)、快取記憶體(Cache)、控流排(Bus)等。
控制單元用來控制與指揮電腦各單元間相互運作、資料傳遞等，主要的功能包括：(1) 負責接受命令與解釋命令。
(2) 負責整部電腦的指揮及控制。
(3) 負責控制程式與資料進入主記憶體。算術邏輯單元目的在負責算術運算與邏輯判斷的工作。主要的功能包括：
(1) 負責電腦系統中的算術(加、減、乘、除)、邏輯比較(比較大小、判斷)工作。
(2) 決定數值運算的速度。暫存器是CPU中暫時存放資料的地方，也是電腦所有記憶單元中存取資料最快的裝置，常見的暫存器有累加器、指令暫存器、位址暫存器、一般用途暫存器、旗標暫存器、程式計數器 。 快取記憶體，包括L1 Cache、L2 Cache，當電腦要執行程式時，必須將所需的資料載入主記憶體中，以供CPU執行的過程中擷取，然而主記憶體的速度無法滿足CPU的需求，因此才有快取記憶體的存在，節省在CPU執行過程中等待資料所需的時間。早期電腦的CPU中只加入L1 Cache，而L2 Cache則建於主機板上，目前新款的CPU已將L1 Cache、L2 Cache內建於CPU中，新增L3 Cache於主機板上溝通CPU與主記憶體。 匯流排是電腦元件間互相傳遞訊息、溝通資料的管道，位於CPU內部的匯流排稱為「內部匯流排」，依照所傳遞訊號的類型又可分為位址匯流排(Address Bus)、資料匯流排(Data Bus)、控制匯流排(Contrl Bus)。 除此之外，在處理器組成中尚有一個部分需要考量，稱為「指令集」。一般而言指令集的結構可以分為兩種，一種稱為「複雜指令集(CISC)」；另一種稱為「精簡指令集(RISC)」。前者既然稱為「複雜」顧名思意，即內建在晶片中的指令數較多，但相對而言讀取指令與解譯指令的時間也較長，執行速度較慢、耗電量較大；後者則只將部份的指令內建於晶片之中，因指令數少，故讀取與解譯指令的速度反而較快，但是若執行到非內建的指令時，因為需要透過數個指令結合成所要執行的指令要求，相對而言執行的速度反而較複雜指令集要來得慢。(3) CPU的運作原理與方式指令或資料進入電腦之後，執行一個指令的過程包括：記憶→擷取(Fetching)→解碼(Decoding)→執行(Executing)→儲存(Storing)等幾個步驟，又稱為指令週期。其中從擷取開始即交由CPU來執行，首先我們先來探討到底這些步驟必須負責那些事。
記憶：已輸入的指令或資料存在記憶單元之中，記憶單元必須提供CPU執行過程中所需要的資料，這邊所看到的記憶單元可廣泛地包括主記憶體、快取記憶體、暫存器等。 擷取：指控制單元由記憶單元中擷取指令或資料。 解碼：主要的動作在「分析指令」，並發出適當的控制訊號以便執行指令。 執行：算術/邏輯單元負責依照傳過來的指令需求，進行算術運算及邏輯判斷的動作。 儲存：控制單元將結果存至內部的暫存器或外部的記憶單元。 舉個例子來說，若我們要計算「(5+6)*7-8」，則在電腦中的運作方式可以簡單地表示如下：
各位可能會想說，電腦怎麼這麼笨，「我一個步驟就可以算出69了，它要執行這麼複雜的處理」。有一個要點大家必須先搞清楚，雖然電腦在算出69的過程中經歷了很多步驟，但是它所用的時間卻是無比的節省，一般而言，電腦執行一個指令的時間，通常僅需要百萬分之一秒(MIPS，million of instruction per second)，甚至更短的時間，反過來說CPU每一秒可執行數百萬個以上的指令。以上述這樣四個步驟的處理，對它而言不用超過0.1秒就可以完成。(4) 常見的CPU規格與種類依照針腳數來作區隔：
之前我們說過CPU背後一根根金針狀的東西我們稱為針腳，每一家公司對於每一種發行的CPU其針腳數卻未必相同，不同的針腳設計，除其定義不同外，對於支援的晶片組及安裝的插槽也不相同。
若以針腳數來區隔的話，CPU的類型可以包括Slot 1、SCOKET 370、SCOKET 478、SCOKET A等。在Pentium早期的封裝方式必須使用的插槽規格為Slot1，它有點像電視遊樂器的卡匣方式，在早期為Intel打下不小的江山。但是這種封裝方式無法有效地解決微處理器在運作時所發出的高熱，價格較高，再加上AMD的嚴厲挑戰下，使得Intel公司不得不選擇較具有挑戰力的「Scoket 370」結構，只是當時並非用在Pentium等級的電腦，而是另一款主打低價市場的「Celeron」處理器。在目前Pentium Ⅳ的世代下，Celeron及Pentium等級的電腦均已演進到SCOKET 478的規格，而這個規格卻也為Intel創下不錯的成績。
相對於Intel公司的不斷變更針腳的規格，AMD公司也有相同的因應策略，從早期的Slot A、Scoket 462、演進到目前的Scoket A，在在均有與Intel相抗衡的意味，不過古諺有云「鷸蚌相爭，漁翁得利」，相信在兩雄相爭的結果，最終得利的還會是身為消費者的你我。
Intel和Amd公司為了要吸引低價市場的民眾並迎合高階使用者的需求，兩家公司在研發的產品均設計高階規格與較低等級兩種，低階等級的機種整體效能也許比不上高階機種，但對一般的使用者而言在操作上已經足以應付所需：
以下介紹幾款目前較新且常用品牌的處理器：
(Athlon XP3200+)
(Athlon 64 3200+)
，存在一個編碼，帶有
個奇偶校驗位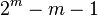
個資料位。該
